Constant Function In Discrete Mathematics

Then let h x denote the function. Greek philosopher aristotle was the pioneer of logical reasoning. Let f and g be functions from the set of integers or the set of real numbers to the set of real numbers.

integral of absolute value of x math limit calulator math formula general math range definition math function military time minutes math multiplying rational functions math x vs y graph math free math worksheets for 6th grade

Pin On Math Magic

Pin By Jorge Colmenares Bazurto On Rick Y Morty In 2020 Logic Math Words Formulas

Pin On Mathematics

Signals And Systems Formula Sheet Tipsntricks In 2020 Studying Math Step Function Laplace Transform

Curve Sketching Calculus Teacher Ap Ab

Mathematics Cheat Sheet Graphing Subtraction

Calculus Limits At Infinity Three Easy Examples

Algebra Domain And Range Doodle Notes With Powerpoint Exponential Functions High School Math Activities

Discrete mathematics propositional logic the rules of mathematical logic specify methods of reasoning mathematical statements.

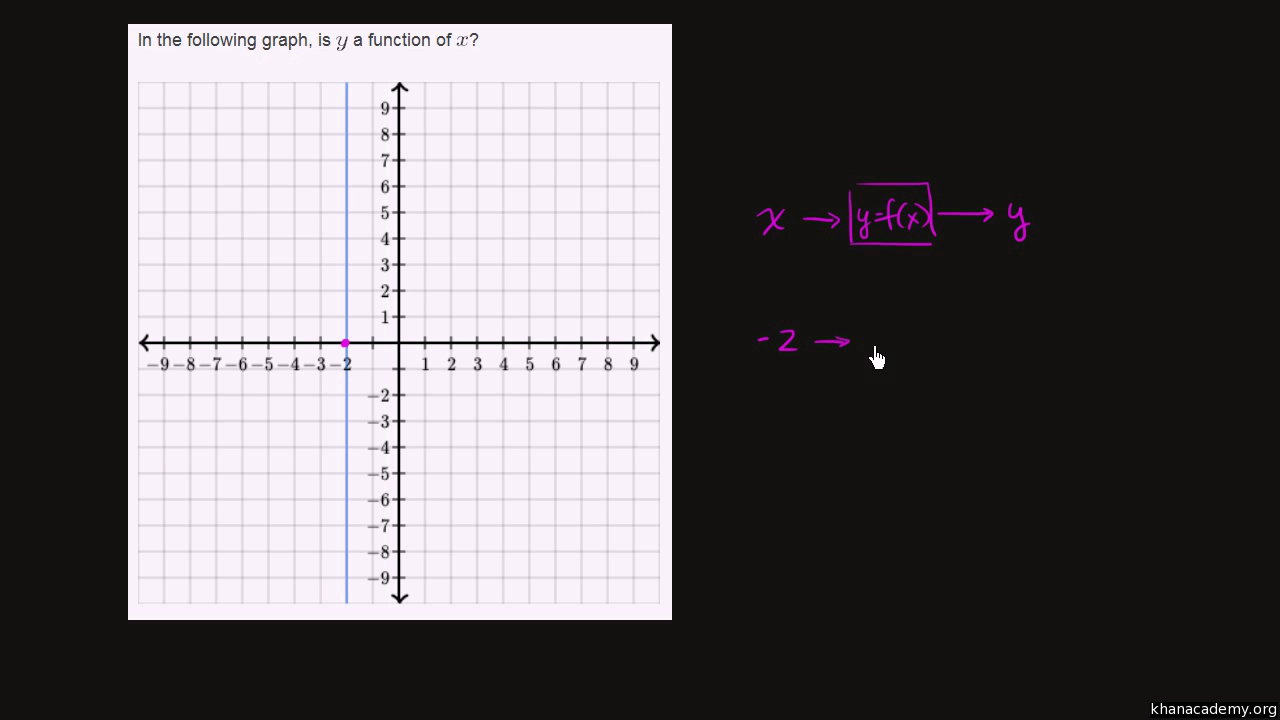
Constant function in discrete mathematics. A function assigns to each element of a set exactly one element of a related set. Here are some common functions listed from slowest to fastest growth. You re confused about the definition of injectivity though. Let a and b be nonempty sets.

For each k ge0 and each a ge0 the constant function c k a mathbb n k to mathbb n is defined by the formula c k a x a text for every element x in mathbb n k in the case k 0 we may identify the function c k a with the number a. So you re right that this is a constant and hence can t be surjective since the codomain mathbb r has more than one point. For example the function is a constant function because the value of is 4 regardless of. Functions definition.

O 1 o log n o n o n log n o n 2 o 2 n o n caution. There are infinitely many functions between each element of this list. H x f circ g x g circ f x a cx d b c ax b d ad b bc d. For example if at one.

A continuous function on the other hand is a function that can take on any number within a certain interval. We say f x is o g x if there are constants c and k such that jf x jcjg x j whenever x k. A function f from a to b is an assignment of exactly one element of b to each element. In other words big o is the upper bound for the growth of a function.

Functions find their application in various fields like representation of the computational complexity of algorithms counting objects study of sequences and strings to name a few. Chapter 2 function in discrete mathematics 1. For example a discrete function can equal 1 or 2 but not 1 5. In mathematics a constant function is a function whose output value is the same for every input value.

Therefore as long as the base b is a constant it differs from log n by a constant factor.