Maximum Error Of Estimate Math

From 48 to 55 25 7 25.

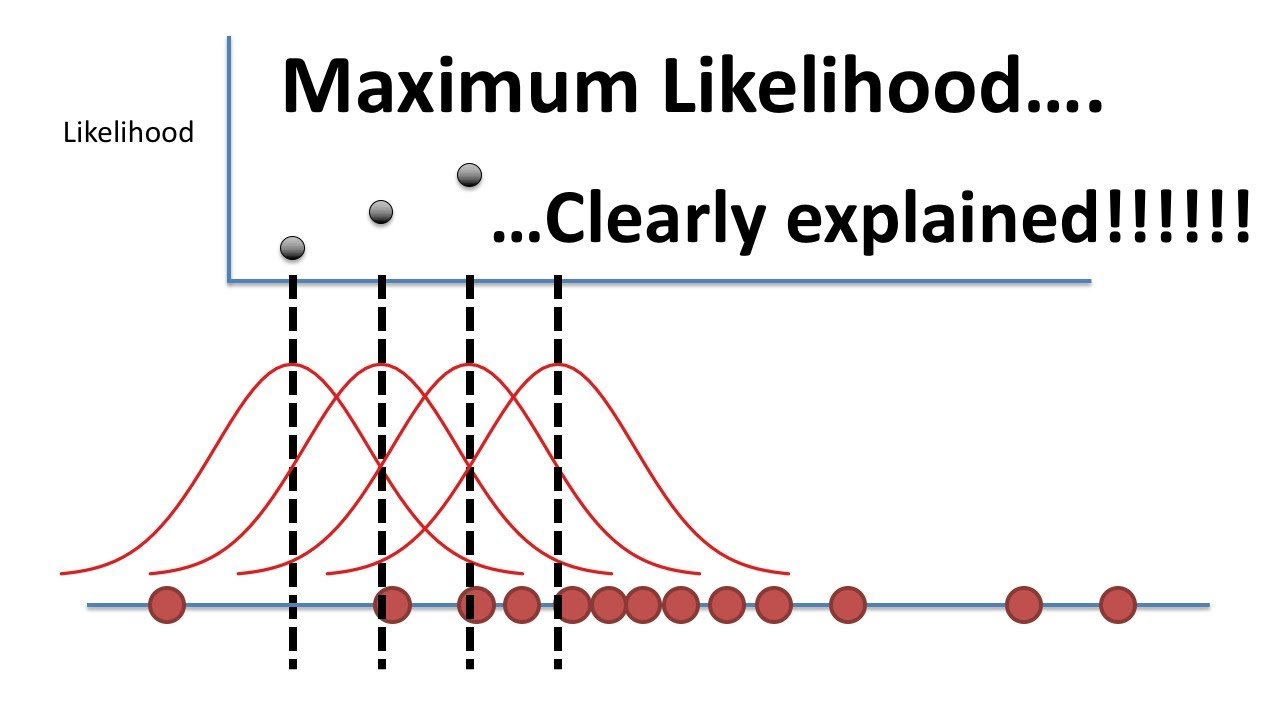
Maximum error of estimate math. It only takes a minute to sign up. The one value we know exactly is f 0 e0 1. Multiplying za 2 to the standard deviation of the sample means. R 4 π 2 x sin.

Which is the absolute error. If one of the sides of a square is misestimated by less than 50 for example the maximum error will presumably occur for angles that are about 40 degrees to the left side of the square. I don t understand how the example went from x π 2 5 to 0 2 5. What s the smallest degree taylor.

Absolute error 7 25 m 2. Estimate the maximum possible error in the approximation. Subtracting za 2 to the standard deviation of the sample means. Percentage error 15 1 which is not very accurate is it.

Absolute relative and percentage error. Relative error 7 25 m 2 48 m 2 0 151. The only tricky thing here is. What should we use for our basepoint.

Pick the biggest one. C o s x t 4 π 2 for x π 2 0 2 π 2 0 2. Mathematics stack exchange is a question and answer site for people studying math at any level and professionals in related fields. We have a magical cube and we measure its side length to be 2.

Z 5. So we will use a taylor polynomial t n x for ex about a 0. However we know our measurement could be inaccurate with max error of 0 1. R 4 π 2 x 1 5.

The maximum error of the estimate is found by a. X π 2 5. Since e e1 we could use a suitable taylor polynomial for the function f x ex to estimate e1. We can then estimate e by computing t n 1.

This video will help you estimate the maximum standard error. Adding za 2 to the standard deviation of the sample means.