Relative Maximum Math Example

F x x 3 3 x 2 9 x 7.

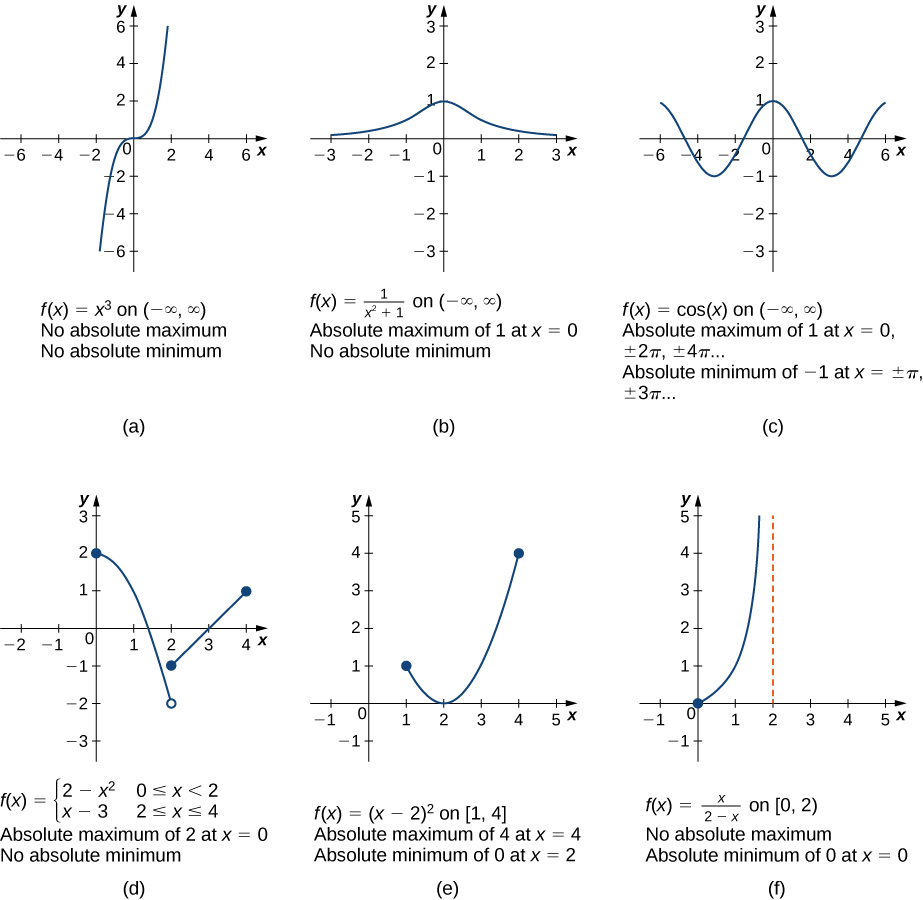
Relative maximum math example. X 4 π 2 π 0 2 π 4 π x 4 π 2 π 0 2 π 4 π. F x 12x3 24x2 12x 12x x2 2x 1 to factorize x2 2x 1 into linear forms we do this. Begin align left 0 0 right. Cosine also has both relative and absolute minimums of 1 at.

According to the definition for a relative maximum. Therefore doesn t that make the specified point a rel. Relative maxima and minima. Relative maximum relative max local maximum local max.

Given the graph of a function find all of its relative maximum and minimum points. Hspace 0 25in d left 0 0 right 8 0 hspace 0 25in f x x left 0 0 right 4 0 hspace 0 25in mbox relative maximum left 2 2 right hspace 0 25in d left 2 2 right 16 0 hspace 0 25in mbox saddle point left 2 2 right hspace 0 25in d left 2 2 right 16 0 hspace 0 25in mbox saddle point end align. A function f x y f x y has a relative maximum at the point a b a b if f x y f a b f x y f a b for all points x y x y in some region around a b a b. Thus to find relative maximum and minimum points we need only consider those points at which both partial derivatives are 0.

Note that this definition does not say that a relative minimum is the smallest value that the function will ever take. This is the currently selected item. F a is rel. Negative increasing or decreasing.

Find the critical points of the function f x 3x4 8x3 6x2 and determine which ones give relative maxima and which ones give relative minima. The first derivative test and the second derivative test are common methods used to find maximum values of a function. X2 2x 1 0 x b p b2 4ac 2a 2 p 4 4 2 2 0 2 1 multiple root so then f x 12x x 1 2. F left parenthesis x right parenthesis equals x cubed plus 3 x squared minus 9 x plus 7.

Cosine has extrema relative and absolute that occur at many points. Let s find the relative extremum points of. Absolute and relative extrema. So if there is a relative maximum at x 0 y 0 z 0 text both partial derivatives at the point must be zero and likewise for a relative minimum.

Cosine has both relative and absolute maximums of 1 at. Maxima when all the x near it are f a f x in the example the specified point lies at a position where the points left of it are all equal to it and the points right of it are less than it. The highest point in a particular section of a graph.