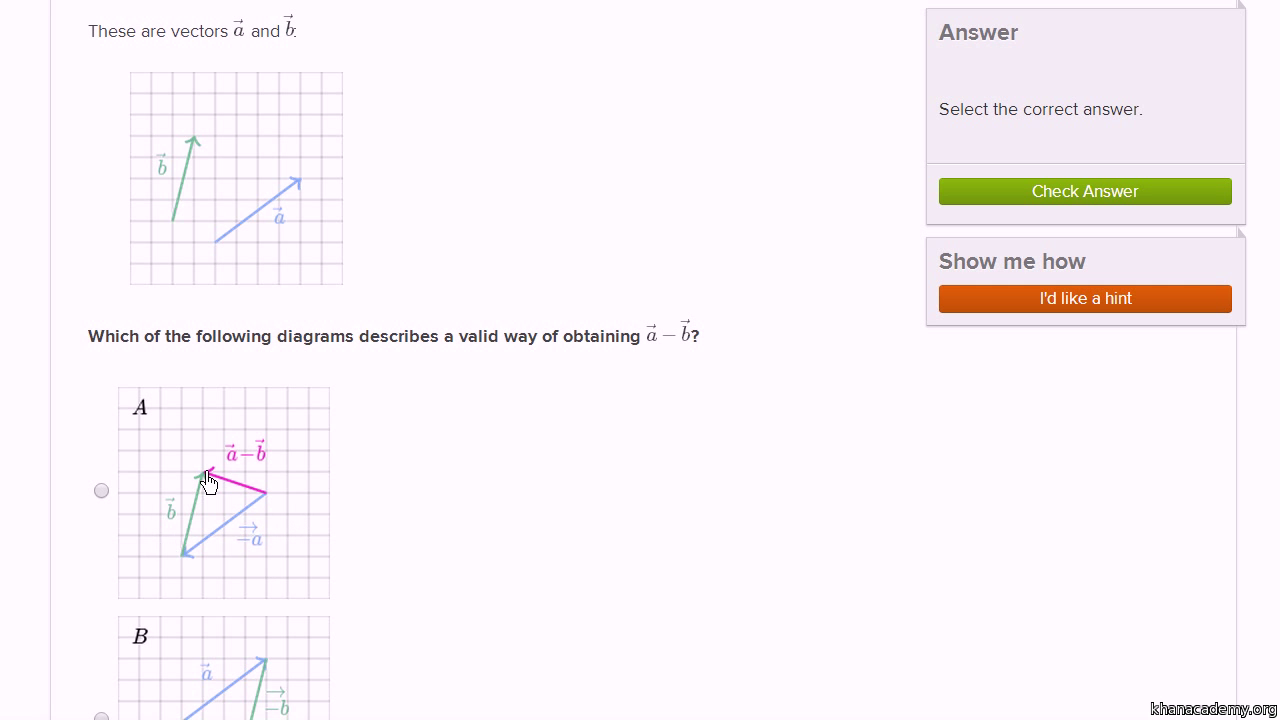
Vector Addition Definition Math

And so forth until all vectors have been added.

Vector addition definition math. Slide v so that the tail of v is on the point of u. X r cos θ 200 cos 60 200 0 5 100. When adding vectors a head to tail method is employed. Adding the two or more vectors using the addition operation gives the resultant vector which is equal to the sum of the two or more vectors.

Y r sin θ 200 sin 60 200 0 8660 173 21. Vector addition is one of the most common vector operations that a student of physics must master. The two vectors a and b can be added giving the sum to be a b. The head of the second vector is placed at the tail of the first vector and the head of the third vector is placed at the tail of the second vector.

100 173 21 84 85 84 85 184 85 88 36. Alternatively the tail of vector a can be joined to the nose of vector b. Y r sin θ 120 sin 45 120 0 7071 84 85. Vectors can be added using the nose to tail method or head to tail method.

X r cos θ 120 cos 45 120 0 7071 84 85. For many specific vector spaces the vectors have received specific names which are listed below. Then draw the arrow which goes from the tail of u to the point of v. Vector addition let u and v be two vectors.

Characteristics of vector math addition. For example if a car is travelling due north at 20 miles per hour and a child in the back seat behind the driver throws an object at 20 miles per hour toward his sibling who is sitting due east of him then the velocity of the object relative to the ground will be in a north easterly direction. This requires joining them head to tail. In this case we are multiplying the vectors and instead of getting a scalar quantity we will get a vector quantity.

In mathematics and physics a vector is an element of a vector space. This is the trickiest of the vector computations we ll be dealing with as it is not commutative and involves the use of the dreaded right hand rule which i will get to. Two vectors a and b represented by the line segments can be added by joining the tail of vector b to the nose of vector a. The definition for the vector s addition can be stated as.

Historically vectors were introduced in geometry and physics typically in mechanics before the formalization of the concept of vector space therefore one often talks about vectors without specifying the vector space to. The process of finding one vector that is equivalent to the result of the successive application of two or more given vectors. We can translate the vector b till its tail meets the head of a.